Active Inference, Active Inference Julia Proposal
ActiveInference.jl Tutorial
The generative model consists of
- A: the observation likelihood model: the matrix {$A=(a_{ij})$} encodes (the agent's beliefs of) the likelihoods (as perceived by the agent) that a state {$i$} generates an observation {$j$}. Given an observation {$j$}, the agent attributes it to some state which presumably generated it, and the particular state {$j$} is understood to have a likelihood {$a_{ij}$} with {$\sum_j a_{ij}=1$}. Suppose the vector {$X$} expresses the observations. Typically, this may be a single observation expressed with a
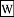one-hot vector. Regardless, the vector {$AX$} expresses, for each state {$i$}, the probability that it is taken to be in that state. This is known as a 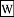categorical distribution.
- B: the transition likelihood model: the tensor {$B=(b_{ijk})$} encodes the (the agent's beliefs of) how a state {$i$} at time {$t$} contributes to the likelihood of a state {$j$} at time {$t+1$} given the agent's action {$k$}.
- C: the preferences over observations (priors over observations): the vector {$C= (c_j)$} encodes the relative weight for an observation that expresses how much the agent likes it (positive) or dislikes it (negative) or is neutral to it (zero) compared to other observations.
- D: the prior over states: the vector {$D=(d_i)$} encodes (the agent's belief of) the initial state of the environment (for example, where it certainly or likely or possibly is in the environment).
- E: the prior over policies (thus, the habits): the vector {$E=(e_{k_1k_2\cdots k_n})$} encodes the likelihood that a policy will be applied. A policy {$E=(e_{k_1k_2\cdots k_n})$} is a sequence of actions {$k_1, k_2, \cdots k_n$} which take place over steps {$1, 2, \cdots n$}.
- A: action selection
- B: backwards pass
- D: final states
- N: neuronal responses
- O: probabilistic outcomes
- P: graphics
- function [MDP] = spm_MDP_VB_XXX(MDP,OPTIONS)
- MDP = spm_MDP_check(MDP); check MDP specification
- handle multiple trials, ensuring parameters (and posteriors) are updated
- set up and preliminaries
- handle multiple trials, ensuring parameters (and posteriors) are updated| for i = 1:size(MDP,2) number of trials, for m = 1:size(MDP,1) number of agents
- set up and preliminaries
- initialise model-specific parameters| for m = 1:numel(MDP)
- ensure any outcome generating agent is updated first
- belief updating over successive time points| for t = 1:T
- loop over models to accumulate Dirichlet parameters and prepare outputs
- Smoothing or backwards pass: replay
- prior Dirichlet parameters
- learning - accumulate concentration parameters
- (negative) free energy of parameters (complexity): outcome specific
- reorganise posteriors for saving
- simulated electrophysiological responses
- assemble results and place in NDP structure
- initialise simulated neuronal respsonses
- simulated dopamine (or cholinergic) responses: assuming a monoexponential kernel
- Belief updating about hidden states: assuming a kernel or impulse response function with a cumulative gamma distribution
Outputs: assemble results and place in NDP structure
- MDP(m).T = T; % number of outcomes
- MDP(m).U = V{m}; % policies
- MDP(m).R = R{m}; % conditional expectations over policies
- MDP(m).C = C(m,:); % utility
- MDP(m).X = X(m,:); % conditional expectations over states
- MDP(m).P = S(m,:); % conditional expectations over controls
- MDP(m).O = O(m,:,:); % outcomes
- MDP(m).v = v{m}; % expected free energy over policies
- MDP(m).w = w{m}; % precision of beliefs about policies
- MDP(m).O = squeeze(MDP(m).O);
- MDP(m).P = squeeze(MDP(m).P);
if OPTIONS.N neuronal responses
- MDP(m).xn = xn(m,:); % simulated neuronal encoding of states
- MDP(m).un = un{m}; % simulated neuronal encoding of policies
- MDP(m).wn = wn{m}; % simulated neuronal encoding of precision
- MDP(m).dn = dn{m}; % simulated dopamine responses (phasic)
1250. Auxiliary functions
- function [G,P,F] = spm_forwards(O,P,A,B,C,H,W,t,T,N,m). deep tree search over policies or paths. This subroutine performs a deep tree search over sequences of actions to evaluate the expected free energy over policies or paths. Crucially, it only searches likely policies under likely hidden states in the future. This search is sophisticated; in the sense that posterior beliefs are updated on the basis of future outcomes to evaluate the free energy under each outcome. The resulting average is then accumulated to furnish a path integral of expected free energy for the next action. This routine operates recursively by updating predictive posteriors over hidden states and their most likely outcomes.
- function [Q,P,F] = spm_backwards(O,P,Q,D,E,a,b,U,m) Backwards smoothing to evaluate posterior over initial states. This subroutine performs Bayesian smoothing in the sense of a replay using variational iterations to optimise posteriors over states, paths and parameters, given the outcomes over an epoch. It effectively implements the prior constraint that certain random variables (i.e., the paths of uncontrollable factors and parameters) do not change with time.
- function A
- function [M,MDP] = spm_MDP_get_M(MDP,T,Ng) returns an update matrix for multiple models. In some applications, the outcomes are generated by a particular model (to maximise free energy, based upon the posterior predictive density). The generating model is specified in the matrix MDP(m).n, with a row for each outcome modality, such that each row lists the index of the model responsible for generating outcomes.
- NOTES: variational approximations to mapping from outcome space to approximate (variational) posterior using spm_VBX
- NOTES: on Dirichlet distributions: illustrating the impact of uncertainty
- and the difference between the log of an expected Dirichlet
- ccomplexity costs and the precision of likelihoods