Entropy, Maximum entropy principle
The formula for entropy: {$S=\sum_i p_i\log \frac{1}{p_i}$}
Let's work with {$\log_2$}.
Entropy examples
Certainty
When there is a single nonzero probability {$p_1=1$} we have {$S= 1 \log 1 = 0$}.
Two states
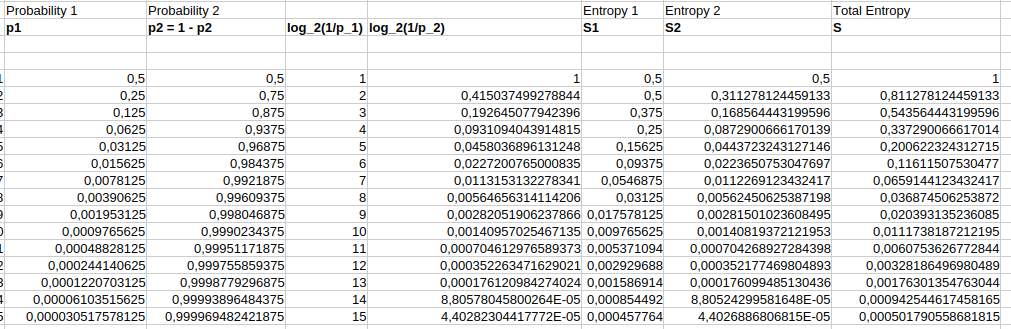
When there are two states, let's consider one state with probability {$p_1=\frac{1}{2^k}$} and the other state with probabilty {$p_2=1 - \frac{1}{2^k}$}.
| {$\mathbf{p_1}$} | {$\mathbf{p_2}$} | {$\mathbf{S=p_1\log_2 \frac{1}{p_1} + p_2\log_2 \frac{1}{p_2}}$} | {$\mathbf{S}$} |
| {$1$} | {$0$} | {$1\log 1 + 0$} | {$0$} |
| {$\frac{1}{2}$} | {$\frac{1}{2}$} | {$\frac{1}{2}\log_2 2 + \frac{1}{2}\log_2 2 = .5 \cdot 1 + .5 \cdot 1 = .5 +.5$} | {$1$} |
| {$\frac{1}{4}$} | {$\frac{3}{4}$} | {$\frac{1}{4}\log_2 4 + \frac{3}{4}\log_2 \frac{4}{3} = .25 \cdot 2 +.75 \cdot .42 = .5 + .31 $} | {$.81$} |
| {$\frac{1}{8}$} | {$\frac{7}{8}$} | {$\frac{1}{8}\log_2 8 + \frac{7}{8}\log_2 \frac{8}{7} = .125 \cdot 3 +.88 \cdot .20 = .375 + .17 $} | {$.54$} |
| {$\frac{1}{16}$} | {$\frac{15}{16}$} | {$\frac{1}{16}\log_2 16 + \frac{15}{16}\log_2 \frac{16}{15} = .063 \cdot 4 +.94 \cdot .09 = .25 + .09 $} | {$.34$} |
| {$\frac{1}{32}$} | {$\frac{31}{32}$} | {$\frac{1}{32}\log_2 32 + \frac{31}{32}\log_2 \frac{32}{31} = .031 \cdot 5 +.97 \cdot .05 = .16 + .04 $} | {$.20$} |