Free Energy Principle, Active Inference, Energy
Ambiguity = Expected Value of Knowledge Gained = Entropy
The expected value of the knowledge gained (information learned, surprisal, self-information, information content) {$I(p)$} of a variable {$Z\in [n]$} is the ambiguity (entropy) {$H(Z)=\sum_{i\in [n]}p_i I(p_i) = \sum_{i\in [n]}p_i\log \frac{1}{p_i}$}.
- Low ambiguity = the knowledge gained is expected to be little
- High ambiguity = the knowledge gained is expected to be large
- No such thing as negative ambiguity. This would mean that knowledge is expected to be lost. Yet life seems to decrease ambiguity, which means knowledge is shed into the environment.
- Probability implies an investigatory window where a question (of what will happen) is replaced by an answer (of what did happen), indicating the passage of time (an event) and implying an observer and their knowledge gained.
- Entropy differs from energy in that {$P(x,y)$} in the latter gets replaced by {$Q(x)$}, yielding a degeneracy whereby nothing is achieved, as when the model equals what it is modeling,
Axioms for {$I(p)$}
| {$I(1)=0$} | If an event is certain, then there is no knowledge gained. |
| If {$p_1 > p_2$} then {$I(p_1) < I(p_2)$} | If the probability increases, then the knowledge gained decreases or stays the same. |
| {$I(p_1p_2)=I(p_1)+I(p_2)$} | The knowledge gained from two independent events is the sum of the knowledge gained from each of them. |
| {$I(p)$} is a twice continuously differentiable function of {$p$} | Knowledge gained, as a function of probability, is twice continuously differentiable. |
Given:
- a finite set {$ [n]$}
- a partition {$E = E_1 \sqcup E_2 \dots E_{r-1} \sqcup E_r$} of {$ [n]$}. Note that {$\sum_{j=1}^r |E_j| = n$}.
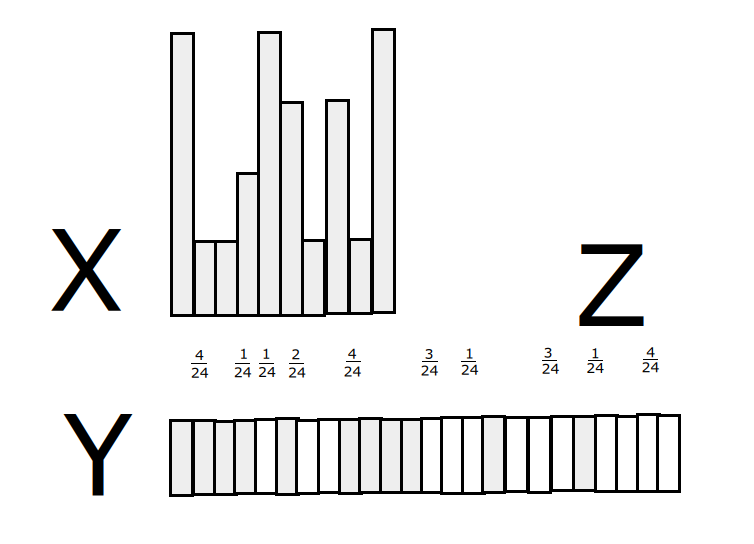
- a uniform distribution {$Y$} on a finite set {$ [n]$}. For all {$i\in [n]$} we have {$Y(i)=\frac{1}{n}$}. Thus {$\sum_{j=1}^r \frac{1}{n} = 1$}.
- a distribution {$Z$} on {$ [n]$} such that for all {$i\in E_j$} we have {$Z(i)=p_j=\frac{|E_j|}{n}$}. Note that {$\sum_{j=1}^r p_j = \sum_{j=1}^r\frac{|E_j|}{n}=1$}.
Note that {$k$} likelihoods of a single value each with probablity {$\frac{1}{n}$} being chosen is equivalent to choosing one of {$k$} values each with probability {$\frac{1}{n}$}. It's just a matter of relabeling.
Therefore:
| {$H[Y]$} | {$=H[Z]+H[Y|Z]$} | By construction. We construct {$Y$} by starting with {$Z$} and consider uniform distributions within each part of {$E$} |
| {$=H[Z]+\sum_{i\in [r]}p_i H[Y|Z=i]$} | The key point: Breaking up the entropy in terms of the probability for each value of {$Z$} | |
| {$=H[Z]+\sum_{i\in [r]}p_i H[Y|Y\in E_i]$} | Rethinking {$Z$} in terms of {$Y$} | |
| {$=H[Z]+\sum_{i\in [r]}p_i(\log |E_i|)$} | the entropy of a uniform distribution is given by the logarithm | |
| {$=H[Z]+\sum_{i\in [r]}p_i(\log p_in)$} | because {$|E_i|=p_in$} | |
| {$=H[Z]+\sum_{i\in [r]}p_i(\log p_i + \log n)$} | log of product is sum of logs | |
| {$=H[Z]+(\log n)\sum_{i\in [r]}p_i + \sum_{i\in [n]}p_i(\log p_i)$} | distributing and pulling out the constant | |
| {$=H[Z]+\log n + \sum_{i\in [r]}p_i\log p_i$} | sum of probabilities is {$\sum_{i\in [r]}p_i=1$} | |
| {$\log n$} | {$=H[Z]+\log n + \sum_{i\in [r]}p_i\log p_i$} | the entropy of a uniform distribution is given by the logarithm |
| {$H[Z]$} | {$=-\sum_{i\in [r]}p_i\log p_i$} | subtracting |
| {$H[Z]$} | {$=\sum_{i\in [r]}p_i\log \frac{1}{p_i}$} | inverting {$p_i$} and removing the minus sign |
Sources